Conformal field theory in momentum space
Developing a new approach to conformal field theory using the momentum-space representation of correlation functions
Conformal field theory
Conformal field theory is a special type of quantum theory in which there is no characteristic length scale: physical laws are the same at all scales, unlike in the real world where the gravitational and electromagnetic forces decrease with distance, and the nuclear force increases.
Even though our world is clearly not of this type, conformal field theory is useful in the effective description of many phenomena, and at critical points of statistical and condensed matter systems. It is also particularly interesting from a mathematical point-of-view, because some conformal field theories can be solved exactly despite being strongly-coupled, using the so-called conformal boostrap.
Trading position for momentum
Traditionally, the conformal bootstrap is formulated using correlation functions of operators with a definite position. However, it can be useful sometimes to use the momenta of operators instead of their positions, a standard practice in particle physics where the main observables are scattering amplitudes.
The momentum-space representation of conformal field theory is still underdeveloped, and it is a long-term project of mine to contribute to its growth. I obtained several important results in this direction.
3-point functions
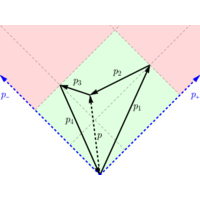
While correlation functions of 3 operators have been known in terms of positions since the 1970’s, the equivalent in terms of momenta was not known until recently. I was among the first people to realize that Wightman functions (a particular type of correlation functions) are actually generalized hypergeometric functions of two variables of the Appell F₄ type, and wrote a couple of papers on this:
- Conformal 3-point functions and the Lorentzian OPE in momentum space (Gillioz, 2020)
- From Schwinger to Wightman: all conformal 3-point functions in momentum space (Gillioz, 2021)
Conformal blocks for 4-point functions
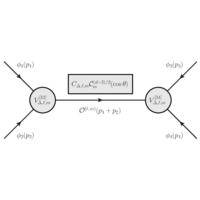
One of the key properties of conformal field theory is that correlation functions of 4 or more operators can be decomposed into (infinite) sums of 3-point correlation functions. I showed that this decomposition takes a particularly nice, factorized form in momentum space in another series of papers:
- Momentum-space conformal blocks on the light cone (Gillioz, 2018)
- Conformal partial waves in momentum space (Gillioz, 2021)
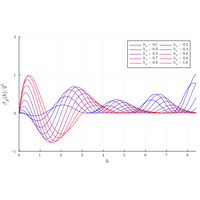
The momentum-space conformal bootstrap in 2d
Finally, the ultimate goal of this project is to formulate a conformal bootstrap directly in momentum space. This has been achieved in two dimensions so far, and I have good hope to extend the results to dimension 3 and higher in the future.
- Convergent Momentum-Space OPE and Bootstrap Equations in Conformal Field Theory (Gillioz et al., 2020)
- The momentum-space conformal bootstrap in 2d (Gillioz, 2025)